最近看一篇 Google 的论文：《Encode, Tag, Realize: High-Precision Text Editing》，看源码的时候发现其前期预处理的时候用了最长公共子序列（Longest Common Subsequence，LCS）算法来生成词汇表。之前只是知道这个算法，但是具体解法并不是很清楚。如果你经常刷题，可能会很熟悉了，但是我对刷题一直保持排斥态度，所以不太懂。趁这个机会来看看这个 LCS。

定义

根据 Wikipedia：

The longest common subsequence (LCS) problem is the problem of finding the longest subsequence common to all sequences in a set of sequences (often just two sequences).

也就是说寻找多个序列（通常是两个）之间的最长的公共子序列，输入是多个序列，输出是一个子序列。还有一个和这个很相似的问题：最长公共子串（Longest Common Substring），和 LCS 的区别就在于子序列不要求连续，而子串是要求连续的，即 subsequence 和 substring 的区别。例如 ABCBDAB 和 BDCABA，最长公共子序列是 BCBA，就是不连续的。

解法

其解法大致有两种：穷举法和动态规划法。

其实还有一种方法是递归法，动态规划法是对其的一种改进（也使用了递归），就暂且不说这种方法了。

以下均以寻找两个字符串之间的 LCS 为例。

穷举

穷举是最直接的方法，也是最耗时的。其思想是：先找到两个字符串中较短的字符串，找出其所有子序列，然后依次查看每个子序列是否在较长字符串中，最后得出一个公共子序列列表，进而得到最长的公共子序列。

主函数如下：

为了尽量保持文章简洁，其他辅助函数未列出，完整代码见文章底部 GitHub 地址。

def lcs_brute_force(s1, s2):
    if len(s1) < len(s2):
        short = s1
        long_ = s2
    else:
        short = s2
        long_ = s1
    cs = []
    for sub in get_all_subsequences(short):
        if is_subsequence(sub, long_):
            cs.append(sub)
    max_len = len(max(cs, key=len))
    return (s for s in cs if len(s) == max_len)

一个长度为 $n$ 的字符串，共有 $2^n$ 个子序列：

$C_n^0 + C_n^1 + C_n^2 + \cdots + C_n^n = \sum_{i=0}^n C_n^i = 2^n$

假设字符串 $X$ 的长度为 $m$，字符串 $Y$ 的长度为 $n$，且 $m > n$，那么寻找其 LCS 就需要先找到 $Y$ 的所有子序列，然后去 $X$ 中查。显然时间复杂度为 $O(2^n)$，指数级的复杂度，这很明显不是一个适合大规模应用的算法。

动态规划

动态规划法（Dynamic Programming，DP）要含蓄得多，并不直接大海捞针式地穷举所有可能，而是根据将这个大问题分解为很多小问题，逐个解决小问题从而得到大问题的解。那么在这里，「小问题」就指的是诸多子串之间的 LCS。

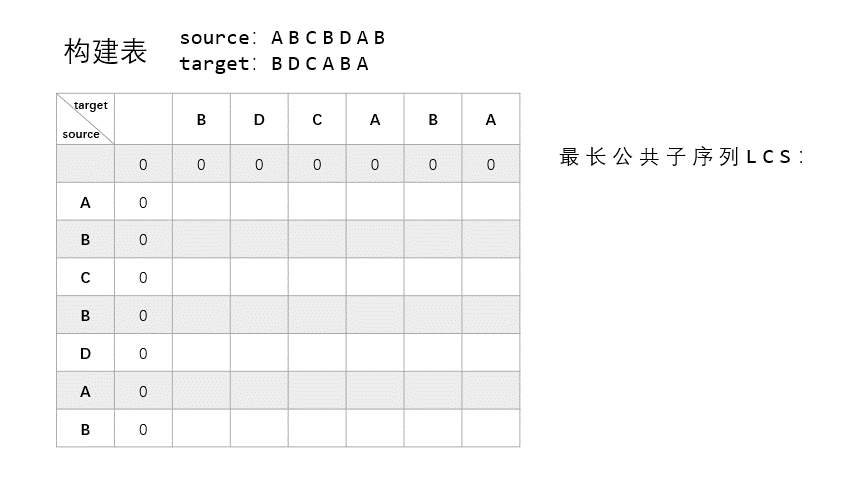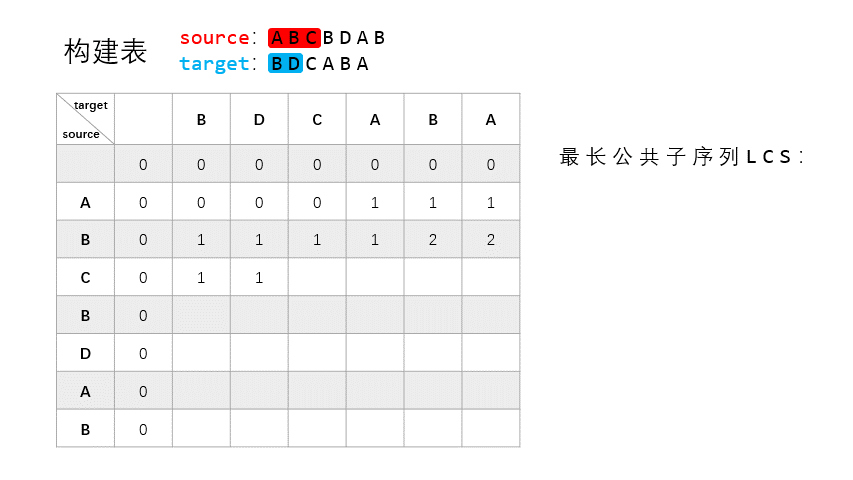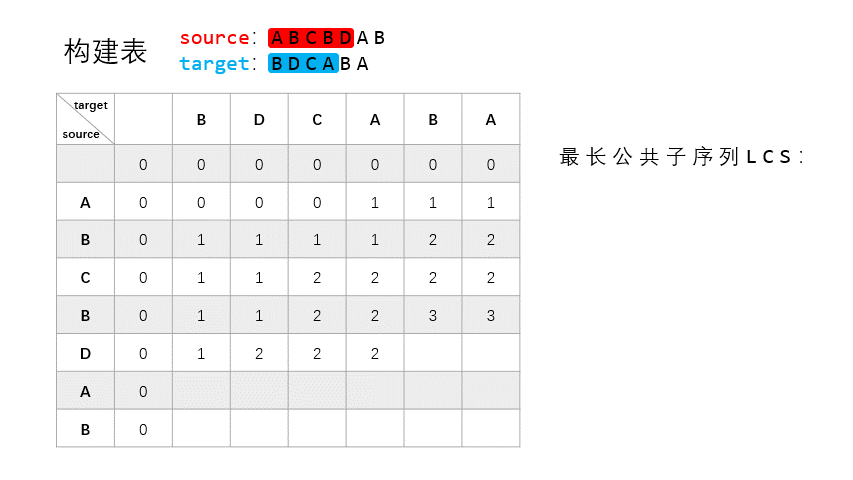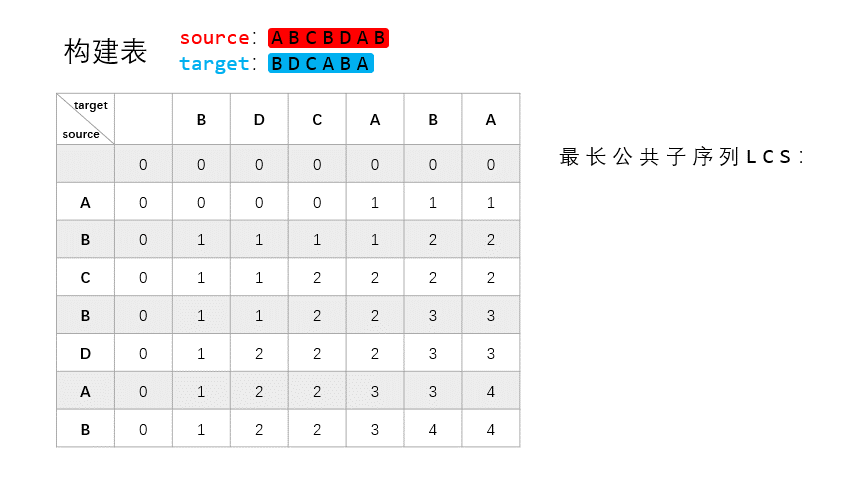
总体上来说，动态规划法的思路分两步走：构建和重建。构建是要构建一个表 $T$，记录 $X_{:i}$ 和 $Y_{:j}$ 之间的 LCS 长度。重建是要根据表 $T$ 去重建恢复具体的 LCS，即具体的字符。

构建

构建部分是基于以下几点的：

若 $X_i = Y_j = t$，则 $t$ 是 $X_{:i}$ 和 $Y_{:j}$ 之间的 LCS 的最后一个字符。
若 $X_i \neq Y_j$，则寻找 $X_{:(i-1)}$ 和 $Y_{:j}$，或者 $X_{:i}$ 和 $Y_{:(j-1)}$ 之间的 LCS，这两者之间的最长者，即为 $X$ 和 $Y$ 的 LCS。

可以看到这其实是一个递归的思路，每次都寻找 $X$ 和 $Y$ 中相等元素加入 LCS，LCS 的长度 +1。这一步结束之后便会生成一个 $(m+1) \times (n+1)$ 的表 $T$，这个表的第一行和第一列是初始值，均为 $0$，其他值记录的是相应子串之间的 LCS 长度。

代码实现如下（来自 lasertagger）：

def lcs_table(source, target):
    """构建表 T。"""
    rows = len(source)
    cols = len(target)
    lcs_table = [[0] * (cols + 1) for _ in range(rows + 1)]
    for i in range(1, rows + 1):
        for j in range(1, cols + 1):
            if source[i - 1] == target[j - 1]:
                lcs_table[i][j] = lcs_table[i - 1][j - 1] + 1
            else:
                lcs_table[i][j] = max(lcs_table[i - 1][j], lcs_table[i][j - 1])
    return lcs_table

为了更直观的展示构建过程，我制作了一个 GIF 来说明：

source 为 $X$，target 为 $Y$。

construct table

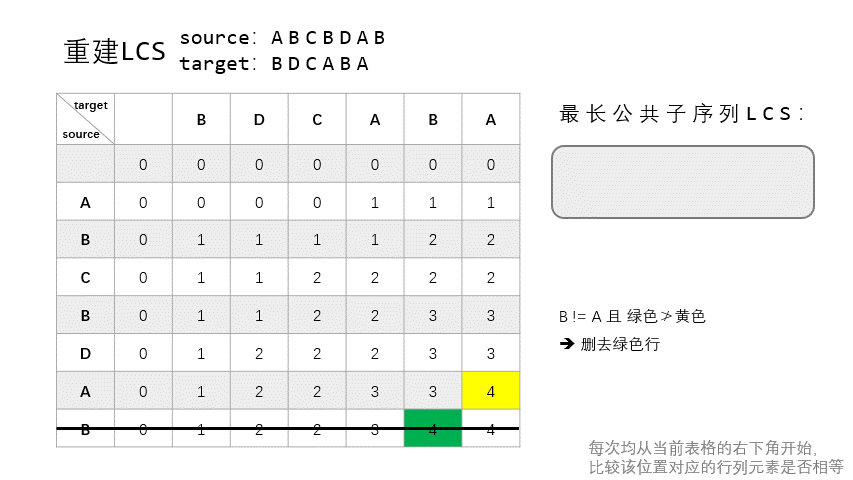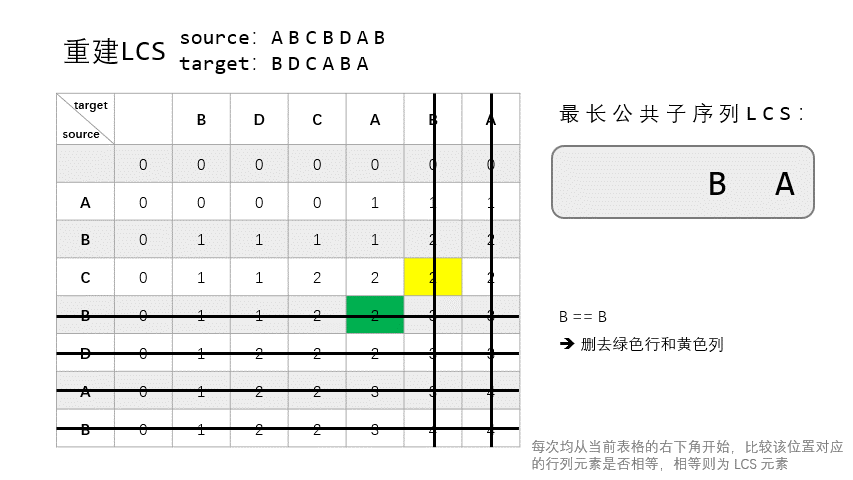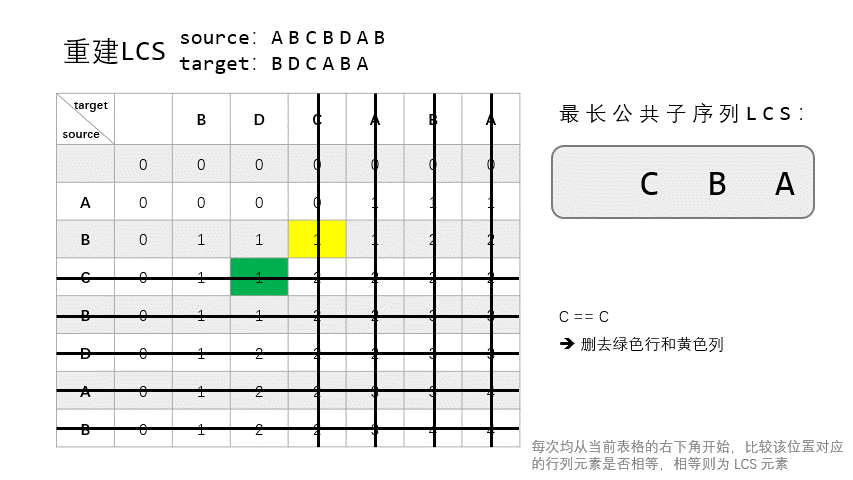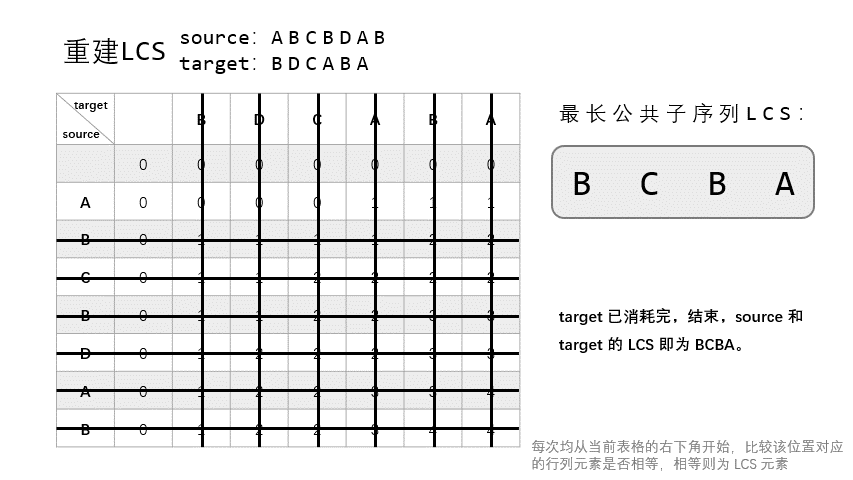
重建

也叫回溯，指从表 $T$ 的右下角开始向上回溯，重建整个 LCS。

记 $\text{LCS}_{X, Y}$ 为 $X$ 和 $Y$ 的之间的 LCS。

回溯时：

和构建时相同，若 $X_{i-1} = Y_{j-1} = t$，则将 $t$ 加入当前 LSC 列表，然后继续从 $T[i-1, j-1]$ 回溯，即向左上方走。
若 $X_i \neq Y_j$：
- 若 $T[i, j-1] > T[i-1, j]$，即 $\text{LCS}_{X_{i}, Y_{j-1}} > \text{LCS}_{X_{i-1}, Y_{j}}$，说明 $\text{LCS}_{X, Y}$ 肯定是包括 $\text{LCS}_{X_{i}, Y_{j-1}}$ 的，所以从 $T[i, j-1]$ 处继续回溯。
- 否则，从 $T[i-1, j]$ 处开始回溯。

代码实现如下（改自 lasertagger）：

def _backtrack(table, source, target, i, j):
    """回溯 LCS 表来重建 LCS。Backtracks the Longest Common Subsequence table to reconstruct the LCS.

  Args:
    table: LCS 表，注意该表的大小为 (len(source) + 1) × (len(target) + 1)。
    source: 源字符串，list 形式。
    target: 目标字符串，list 形式。
    i: 当前行的索引。
    j: 当前列的索引。

  Returns:
    LCS 列表。
  """
    if i == 0 or j == 0:
        # 如果i或者j为0，则说明有一方已经是空字符串，此时直接返回空
        return []
    if source[i - 1] == target[j - 1]:  # 为什么不是 source[i] 和 target[j] 呢？实际上就是，因为 table 表的大小是要比实际 source 和 target 长度大 1 的，所以要减 1，不然就 index out of range 了。
        # Append the aligned token to output.
        # 如果 source[i - 1] 和 target[j - 1] 相等，则表示该值便是当前的 source 和 target 的 LCS 的最后一个 token，
        # 然后 source 和 target 分别往前推一个 token 再去寻找，也是一个递归的过程
        return _backtrack(table, source, target, i - 1, j - 1) + [target[j - 1]]
    if table[i][j - 1] > table[i - 1][j]:
        # 如果不相等的话，接下来就是寻找相等的元素，这些元素才可能属于 LCS。
        # 如果不等且 source[:i] 和 target[:j-1] 的 LCS 长度，大于 source[:i-1] 和 target[:j] 的 LCS 长度，
        # 那么就从 source[:i] 和 target[:j-1] 寻找相等的元素
        return _backtrack(table, source, target, i, j - 1)
    else:
        # 和上面同理
        return _backtrack(table, source, target, i - 1, j)

同样为了直观理解，我制作了一个 GIF：

source 为 $X$，target 为 $Y$。

reconstruct

LCS 并不一定唯一

以上图中的两个字符串为例，ABCBDAB 和 BDCABA 之间的 LCS 并不唯一，共有 ['BDAB', 'BCAB', 'BCBA'] 三个，穷举法可以都找到。然而上述的动态规划法却只能找到其中一个。

为什么？

两个数的大小存在三种情况，然而在判断 $T[i, j-1]$ 和 $T[i-1, j]$ 的大小时，上述算法只是比较前者是否大于后者，而相等和小于的情况被同等对待。这就造成了不能找到全部 LCS 的情况。

若 $T[i, j-1] = T[i-1, j]$，说明 $\text{LCS}_{X_{i}, Y_{j-1}}$ 和 $\text{LCS}_{X_{i-1}, Y_{j}}$ 都有可能是 $\text{LCS}_{X, Y}$ 的一部分，因此需要分两条路走，然后合并两条路得到的结果，这样就可以得到全部的 LCS。

构建部分不用改动，重建部分我用一个简单的树结构来存储 LCS 字符，对上述结构进行了改造：

class Tree:
    """一个简单的树结构。"""
    def __init__(self, data=None, left=None, right=None):
        self.data = data
        self.left = left
        self.right = right


def backtrack(table, source, target, i, j):
    """改造的回溯函数。"""
    tree = Tree()
    if i == 0 or j == 0:
        return Tree()
    if source[i - 1] == target[j - 1]:
        tree.data = target[j - 1]
        tree.left = backtrack(table, source, target, i - 1, j - 1)
        return Tree(
            data=target[j - 1], left=backtrack(table, source, target, i - 1, j - 1)
        )
    if table[i][j - 1] > table[i - 1][j]:
        return Tree(left=backtrack(table, source, target, i, j - 1))
    elif table[i][j - 1] == table[i - 1][j]:
        left = backtrack(table, source, target, i, j - 1)
        right = backtrack(table, source, target, i - 1, j)
        return Tree(left=left, right=right)
    else:
        return Tree(right=backtrack(table, source, target, i - 1, j))

重建完这个「树」之后，对齐进行类似 NLR（前序）的遍历即可得到全部 LCS：

由于节点默认的 data 为 None，因此遍历结束后需要去除这些 None，详细可见 GitHub 完整代码。

def traverse_tree(root):
    if root is None:
        return []
    if root.left == None and root.right == None:
        return [str(root.data)]
    return [
        str(root.data) + p for p in traverse_tree(root.left) + traverse_tree(root.right)
    ]

完整代码

见 GitHub。

理解最长公共子序列算法

目录

定义

解法

穷举

动态规划

构建

重建

LCS 并不一定唯一

完整代码

Reference

END

Alan Lee